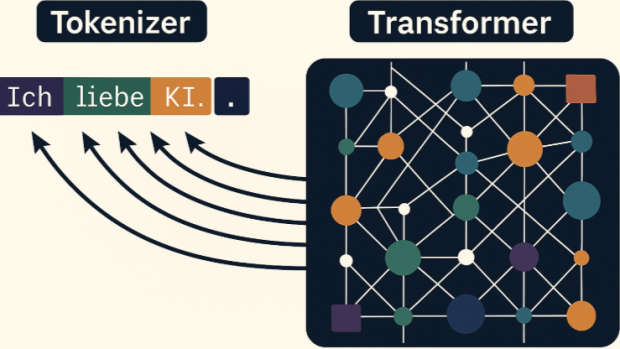
In Diskussionen über Sprachmodelle fällt das Wort „Transformer“ beinahe reflexhaft. Man spricht über Attention, über Layer, über Billionen Parameter. Doch das eigentliche Genie liegt nicht in der Architektur, sondern davor: im Tokenizer.
Denn der Transformer kann nur berechnen, was der Tokenizer zuvor definiert hat. Er denkt nicht in Wörtern, nicht in Sätzen, nicht in Konzepten, sondern in numerisch kodierten Fragmenten sprachlicher Realität.
Der Tokenizer ist die epistemische Linse, durch die eine Maschine die Welt überhaupt erst sehen kann.
Von Zeichen zu Bedeutung
Der Tokenizer übersetzt Sprache, Code oder Zahlen in diskrete Einheiten – Tokens. Diese Tokens sind keine Wörter, sondern Bytefolgen, deren Segmentierung aus Häufigkeit und Kontextinformation gelernt wurde. Ein einfacher Satz, wie:
Ich liebe KI. wird beispielsweise zu:
["Ich", " liebe", " KI", "."]
→ [464, 306, 11789, 13] Das mag trivial wirken, ist aber die Grundlage maschinellen Verstehens. Denn derselbe Mechanismus funktioniert ebenso für HTML, Programmcode oder mathematische Ausdrücke:
<div class="box"> → ["<", "div", " class", "=", "\"box\"", ">"]
x = 42 → ["x", " =", " 42"]
心 → ["心"] Das Modell sieht überall nur Sequenzen von Token-IDs, eine universelle Sprache aus Zahlen, die gleichermaßen natürliche Sprache, Symbolik und Syntax kodiert. Das ist die eigentliche Genialität: nicht der Transformer, sondern die Quantisierung der Sprache selbst.
Man beachte, dass die Leerzeichen teilweise dem Token zugeordnet werden. Außer am Satzanfang und am Satzende. Trotzdem, die symbolische Bedeutung der einzelnen Zeichen geht verloren. Daher kann GPT auch nicht zählen, wie viele r das Wort Strawberry hat. Außer, man trickst mit dem Tokenizer ein wenig.
Warum GPT nicht wirklich rechnet
Die Tokenisierung hat allerdings auch ihre Schattenseiten. Zahlen sind keine kontinuierlichen Größen, sondern diskrete Symbole. „42“ ist ein einziges Token, es steht nicht in einem numerischen Verhältnis zu „41“ oder „43“. Das Modell kann also keine numerischen Operationen durchführen, weil die numerische Struktur bereits beim Tokenizing zerstört wird. Es müsste diese Beziehung erst wieder lernen. In symbolischen Systemen wäre diese Beziehung explizit hinterlegt, im neuronalen System muss sie emergent aus Korrelationen rekonstruiert werden. Größere Zahlen werden oft in 3er-Gruppen von Ziffern zerlegt. Eine kluge Darstellung für Sprache, eine schlechte Darstellung für Mathematik. Das BPE-Verfahren behandelt numerische Blöcke nicht als kontinuierliche Werte, sondern als häufige Zeichenmuster, wodurch jede arithmetische Struktur verloren geht.
Das erklärt, warum GPT häufig bei Rechenaufgaben scheitert: Es sieht keine Zahlen, sondern Wörter mit Zahlenbedeutung. „42“ ist für das Modell ähnlich wie „Katze“, ein Token mit Kontext, nicht mit Arithmetik.
Interessanterweise ist dieses Defizit nicht rein maschinell. Auch Menschen denken über Zahlen tokenisiert. „42“ ist kulturell aufgeladen, als Meme, als Symbol, als literarische Konstante. Andere Sprachen illustrieren diese Segmentierung besonders deutlich: Das französische „quatre-vingt-dix“ (wörtlich „viermal zwanzig und zehn“) oder das japanische „hyaku“ (百 für 100) zeigen, dass auch menschliches Zahlverständnis nicht linear, sondern linguistisch kodiert ist.
Wir denken über Zahlen, wie der Tokenizer sie sieht: als sprachliche Einheiten, nicht als Mengen.
Von Wahrscheinlichkeiten zu Fragmenten
Das Training eines Sprachmodells basiert auf der bedingten Verteilung
P(ti ∣t1 , t2, …, ti−1)
der Wahrscheinlichkeit, dass ein bestimmtes Token ti als Nächstes folgt. Doch diese Wahrscheinlichkeit existiert im Modell nicht als analytische Funktion. Sie wird approximiert durch eine Vielzahl gewichteter Matrizen, deren Aktivierungen über Gradientendeszente so lange angepasst werden, bis die Differenz zwischen Vorhersage und tatsächlichem nächsten Token minimiert ist.
Was bleibt, ist kein probabilistischer Raum, sondern ein deterministisches Feld nicht linearer Approximationen. ReLUs eliminieren negative Aktivierungen und brechen damit Symmetrien. Damit wird jede probabilistische Interpretation systematisch zerstört, was bleibt, ist ein deterministisches Aktivierungsmuster, das sich nur noch statistisch deuten lässt. Dropout deaktiviert zufällig Neuronen und fragmentiert den Signalfluss.
Die oft zitierte Formel P(W∣C), die Wahrscheinlichkeit des nächsten Wortes W im Kontext C, existiert im trainierten Modell nicht mehr explizit. Sie ist lediglich die Zielfunktion des Lernprozesses, deren Spur sich in der Topologie der Gewichtsmatrizen verliert.
Das Ergebnis ist ein fragmentierter Aktivierungsraum, in dem Bedeutung als stabiler Attraktor entsteht, nicht als Wahrscheinlichkeitsverteilung. Das Modell konstruiert Kohärenz ohne Wahrheitszugang, es berechnet Konsistenz, nicht Realität.
Wie der Tokenizer Bedeutung ermöglicht
Der Transformer selbst ist architektonisch blind. Er multipliziert Matrizen, aggregiert Gewichte, verteilt Aufmerksamkeit. Aber was er tatsächlich „sieht“, hängt vollständig von der Tokenisierung ab.
Wenn der Tokenizer entscheidet, dass „magisch“ in „mag“ und „isch“ zerlegt wird, dann entsteht Bedeutung auf der Ebene dieser Fragmente, nicht des Wortes. Das Embedding jeder dieser Subtokens wird im Training über Millionen Kontexte hinweg angepasst. Ihre semantische Nähe ergibt sich aus der Korrelation ihrer Aktivierungen mit anderen Tokens.
„Hund“ ist kein Symbol, sondern eine Abfolge von Tokens wie [“H”, “und”], deren Koaktivierungen sich mit anderen Tier-bezogenen Tokens stabilisieren. „Schraubenzieher“ besteht aus [“Sch”, “rau”, “ben”, “zie”, “her”], deren Aktivierungspfade in Clustern erscheinen, die mit Werkzeugbegriffen korrelieren.
Semantik entsteht nicht auf der Wortebene, sondern als mehrschichtige Interferenz im hochdimensionalen Embedding-Raum. Der Tokenizer definiert die Atome, aus denen diese Semantik gebaut wird.
Der eigentliche Durchbruch
Der Tokenizer ist damit kein Vorverarbeitungsschritt, sondern das epistemische Fundament der gesamten Sprachintelligenz. Aber auch seine natürliche Grenze.
Er komprimiert die Welt in endlich viele Symbole, deren Dichte und Segmentierung bestimmen, welche Realität das Modell überhaupt lernen kann.
Es gibt Ansätze, die auf der Bedeutung einzelner Zeichen ansetzen. Allerdings haben diese auch einen viel höheren initialen Trainingsaufwand, um die Bedeutung ganzer Wörter zu verstehen.
Ein anderer Tokenizer, ein anderes Weltbild. Ein Tokenizer, der Zahlen nicht segmentiert, erzeugt ein Modell, das nicht rechnen kann. Ein Tokenizer, der Satzzeichen ignoriert, erzeugt ein Modell ohne Syntaxverständnis. Ein Tokenizer, der Zeichen falsch auftrennt, zerstört Semantik, bevor sie entstehen kann. Ein Modell ohne Tokenizer konvergiert aktuell nicht.
Der Transformer wäre dann ein Rechenwerk ohne Sprache, eine lineare Algebra über Rauschen.
Der Tokenizer bildet die Grenzfläche zwischen Sprache und Zahl, zwischen Syntax und Semantik. Seine Effizienz liegt darin, dass er Bedeutung komprimiert, bevor sie überhaupt verstanden wird. Er ist damit nicht nur das technische Fundament der modernen Sprachmodelle, sondern auch ihr erkenntnistheoretischer Rahmen.